Through a statistical mechanism lens, magnetism can be explained by a lattice of binary spins that can range from a completely random arrangement to total alignment. The percentage of alignment determines the magnetization of the material. These spins are typically denoted as up (+1) or down (-1), and the energy states of the system are defined by an equation involving the spin values, the applied magnetic field, and the interaction strength between neighboring spins. These energy states can be averaged to calculate a total energy or magnetization of the system. Exact mathematical solutions have been defined for the first and second dimensions, but the third dimension continues to elude mathematicians. However, computer simulation makes it possible to model the behavior of magnets in any dimension in various applied magnetic fields at different temperatures.
The spin model is a useful framework for understanding magnets ranging from permanent to paramagnetic. A permanent magnet is one which has magnetization even when no external field in applied. In fact, these magnets are often used to create the magnetic fields that control the behavior of the magnetic nanoparticles that we talk so much about. Those magnetic nanoparticles are paramagnetic, meaning that at zero applied field they are not magnetic at all, but they become magnetic when an external field is applied. How does this happen?
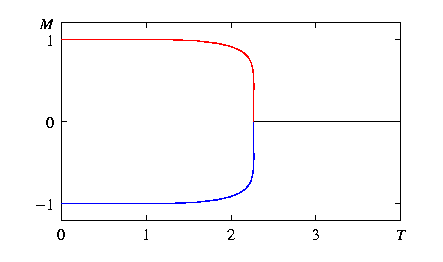
In the Ising model, magnetization is explained by spin alignment. A permanent magnet is made of a material such that the spins spontaneously align with each other at zero applied magnetic field at temperatures below the critical point or Curie Temperature. Above the critical temperature, where thermal disorder reigns, there is no net alignment of spins and the total magnetization is zero. As the temperature drops below the critical point, a drive to decrease free energy reigns and long range order appears as spins spontaneously begin to align. As temperature continues to decrease, the spins continue to align, and this alignment produces magnetization. The spins are always completely aligned at absolute zero, and can be aligned all at 1 or all at -1, but as seen in the graph below the spins often align before absolute zero is reached.
Paramagnetic materials don't display spontaneous magnetization below their critical temperature at zero applied field, but they can have magnetization as external magnetic fields are applied. The external field pulls the individual spins into alignment, and this order is what creates magnetization. When all of the spins are aligned the material is said to be at its saturation magnetization, meaning that the material will not become more magnetic even if a stronger magnetic field is applied.
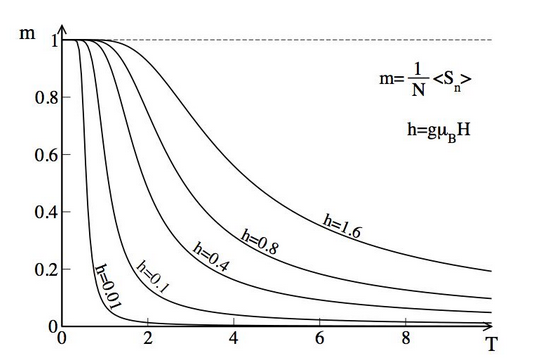
Below: 1-D Ising model for a paramagnet at varying applied magnetic fields (H). Magnetization (m) vs Temperature (T).
Related news:
- Reversibly Binding Immunomagnetic Beads
- The 20th Annual International Conference on Magnetism
- Tumor Depletion with Combined Magnetic Hyperthermia and Photodynamic Therapy